如果想要測量向心力的話,大多間接地測量物體做圓周運動時,該物體的速率、質量及圓周半徑,利用如下關係
向心加速度=運動速率平方 / 運動半徑
再由F=ma算出向心力。
如果,如果只是單純想要直接量呢?想要更直覺看到半徑、線速率與向心力的變化呢?有沒有這樣的設計空間...
於是利用空堂做出了
滾珠軸承的安裝是為了減少晃動與減少繩子跟管口的摩擦。
做好了來試試吧!
所的結果分析如下
後記:
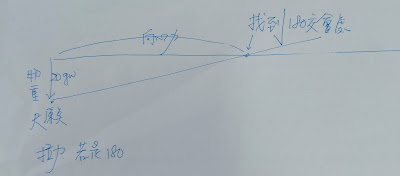
理論上這種旋轉物體一定繩子拉力一定包含物體所受向下重力跟水平向心力作用才對對吧,繩子理論上不可能水平,要處理的話,以國中生而言,我傾向用幾何作圖處理,,不要用複雜計算,舉例說明,物重20gw,若向心力180gw,作圖如下,逆推找出向心力長度換算大小
若是操作時,調整速度讓物重跟拉力值接近1/6,此時繩角度應接近10度,力圖的sin值約為0.17,cos值就會來到0.98以上,在此狀況下,彈簧拉力值與水平分力十分相近,亦即向心力與彈簧讀數相當接近。相關函數資料可參考維基百科三角函數表
若將測試所得的彈簧讀數與向心力理論值對照,會發現確實有相同向心力下,半徑越小速度越快的趨勢,但偏差頗大,但是能量化處理,算是一個起點,學生能動手操作並看到數字,也是多元學習方式的體現,後面有機會,再來設法減小偏差值。



沒有留言:
張貼留言
注意:只有此網誌的成員可以留言。